在泛函分析中,卷积 (Convolution) 或叫旋积、摺积是通过两个函数 $f$ 和 $g$ 生成第三个函数的一种数学算子,表征函数 $f$ 与经过翻转和平移的 $g$ 的重叠部分的面积。若 $f$ 与 $g$ 在 $\mathbb{R}$ 上可积,则数学上的公式为:
\[Cov(x) = \int^{\infty}_{-\infty} f(\tau)g(x-\tau)d\tau \tag{1}\]下面这张图可以简单清晰的看到在电路分析中,卷积运算表示的意义:
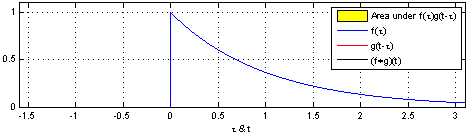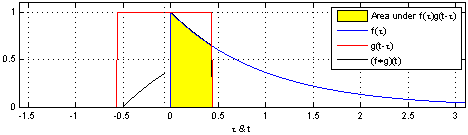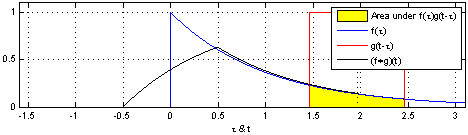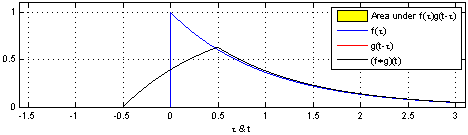
图示方形脉冲波和指数衰退的脉冲波的卷积(后者可能出现于RC电路中),同样地重叠部分面积就相当于”t”处的卷积。注意到因为”g”是对称的,所以在这两张图中,反射并不会改变它的形状。图片来源 Wikipedia
图像处理中卷积运算与这种滑动后求面积的运算极为相似,下面我们来看这个线性系统中的运算方式
卷积与卷积核
在计算机视觉和图像处理中,卷积中的“滑动函数”被称为卷积核(Kernel),在信号处理中也成为滤波(Filter),而且用的是线性滤波,即输出像素是输入领域像素的加权和。下面这个图就清晰的表达了这个运算:
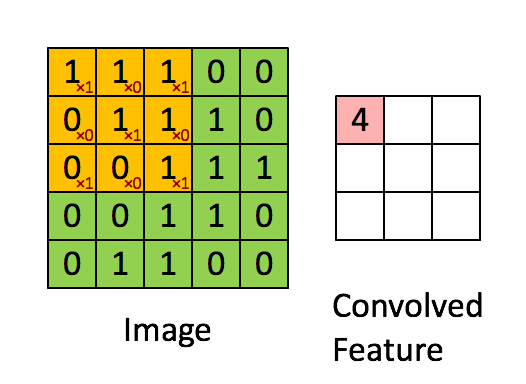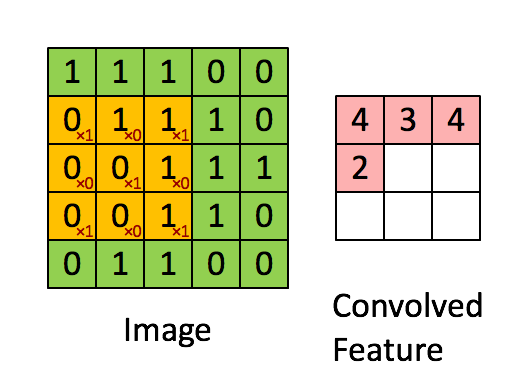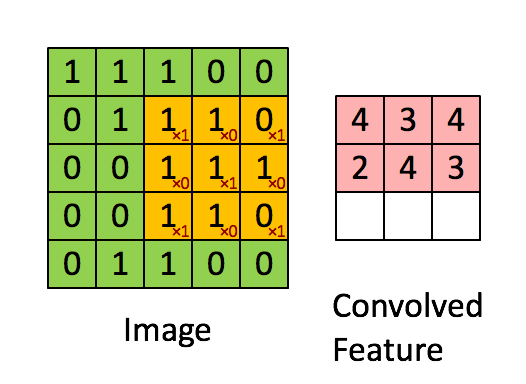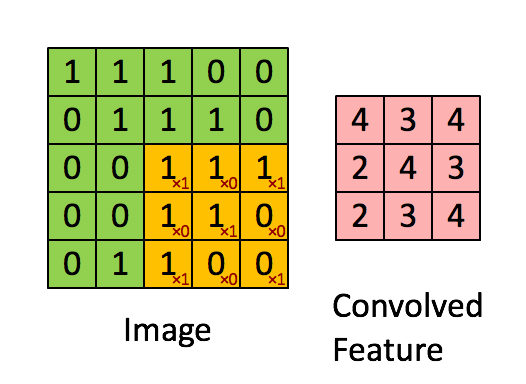
A good picture is more than 1000 words
那这个核可以用来干什么呢?下面举一些直观的例子来看一下卷积运算在图像处理中的应用。处理图像当然要拿出这位美女 Lena 了。

The First Lady of Internet
下面列举出一些常见的卷积核,这几个卷积核是在 Gimp 的官方文档中看到的,不得不说这个开源神器是在强大,还提供自己加卷积处理图像的例子。

Filters>Generic>Convolution Matrix就可以找到这一功能
文档中列举出的五个卷积核分别会锐化(Sharpen)、模糊(Blur)、边缘增强(Edge enhance)、边缘检测(Edge detect)、凸印(Emboss)原始图像。对应的核如下:
\[\begin{array}{ll} Sharpen = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0\\ 0 & -1 & 5 & -1 & 0\\ 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} & Blur = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 & 0\\ 0 & -1 & 5 & -1 & 0\\ 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \\[1em] Edge_{enhance} = \begin{bmatrix} 0 & 0 & 0\\ -1 & 1 & 0\\ 0 & 0 & 0\\ \end{bmatrix} & Edge_{detect} = \begin{bmatrix} 0 & 1 & 0\\ 1 & -4 & 1\\ 0 & 1 & 0\\ \end{bmatrix} \\[1em] Emboss = \begin{bmatrix} -2 & -1 & 0\\ -1 & 1 & 1\\ 0 & 1 & 2\\ \end{bmatrix} & \\ \end{array}\]可惜我没有装 Gimp,所以我在 Matlab 中写了一个小程序做了一下小体验,感觉很不错:
img = imread('lena-origin.jpg');
img = im2double(img);
% im2double will convert unit8 (0-255 integers) value to a double in 0~1, but double will convert it to a same number in double format.
[m,n] = size(img);
[p,~] = size(filter);
mg_new = zeros(m,n);
for i = 1:(m-p+1)
for j = 1:(n-p+1)
img_new(i,j) = sum(sum(img(i:i+p-1,j:j+p-1).*filter));
end
end
% img_new = img_new/max(max(mg_new));
% if values in img_new mostly beyond 1, they need to be adjusted blow 1.
img_new = im2uint8(mg_new);
imshow(img_new)
代码中的 filter 就是卷积核矩阵。当然,Matlab 读取灰度图后数据类型是 uint8,要参与运算需要转为 double 型,这里我用的是 im2double() 函数进行转换,与 double() 函数会有不同的是前者将 0-255 的整数转换到 0-1 的小数,而后者是直接把整数型转换为浮点型。这样会有有些核在求和后大量像素的 double 值大于 1,使得用 im2uint8() 函数转回整型数据后都大于 255,图片会是一片白,我使用的调整策略是简单的归一了一下,不知道这方面有没有什么更好的方案。
话说回来,使用文档中介绍的五种核得到的结果如下:

五种核表现出的直观理解
最后,其实很容易发现,经过卷积运算后会使得结果矩阵比原矩阵要小,一般在图像应用里面会使用外插或者其它方法补齐。
卷积神经网络
卷积神经网络 (Convolution Neural Networks) 在深度学习中有着举足轻重的地位,尤其是应用到图像分类 (Image Classification) 中是取得了很大的突破,例如 Facebook 中的图片自动标注。当然最近也有人将它运用到自然语言处理中 (Natural Language Processing)1, 下面我们来看看一个典型的卷积神经网络的结构。
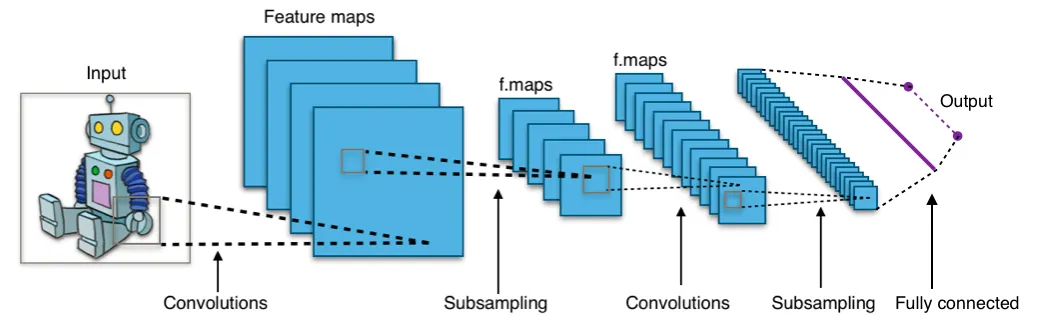
一个典型的神经网络,其中包含两个卷积层,两个子采样层。图片来源 Wikipedia
在传统的深度神经网络中,使用的仅仅是在感知机基础上的深度网络,每一层都是全连接层 (Full connected layer) 或者叫仿射层 (Affine layer),但是由于参数太多,例如一个 $100\times100$ 的图像,就可以表示为一个长度为 $10000$ 的向量,如果在第一个隐藏层的节点数和输入层一样,那么需要的参数就要 $10000\times10000 = 10^{8}$ 个参数,导致训练量非常大,而且过多的参数还非常容易过拟合 (over-fitting)。
而 CNN 则是作为局部连接,通过共享参数,大大减少了参数的训练量。而且在图像处理中通过接受局部信息,还可以学习到图片的物体边缘和形状特征。下面来拆分说明上图中的两种隐藏层的意义。
卷积层
我们已经知道,一个卷积核会将图片生成为另一幅图像。所以我们在每个卷积层使用多个不同的卷积核组成一个卷积核组,不同的核在输入图片上的运算会得到不同的结果,就相当于一张图像的不同通道。当然这些卷积核组我们可以自动的学习出来。在此之后对于每个通道我们都会在后面加上非线性的激励函数。一般来说是 RELU、sigmoid 或者是 tanh 函数,加上非线性的激励函数就是给系统加上非线性因素,因为线性模型的表达能力往往不够2。

一个使用 RELU 作为激励函数的 CNN 网络
实际上,在 1962 年 Hubel 和 Wiesel 通过对猫视觉皮层细胞的研究,提出了感受野 (receptive field) 的概念,1984 年日本学者 Fukushima 基于感受野概念提出的神经认知机 (Neocognitron) 可以看作是卷积神经网络的第一个实现网络,也是感受野概念在人工神经网络领域的首次应用。
这里要注意的是,在下一层的卷积运算中,需要把上一层的卷积核组算得的多个通道进行合并后对下一层的卷积核组进行运算,得到下一层的卷积结果。
池化
池化 (Pooling) 又被称为下采样 (downsampling),因为在利用卷积获得学习的特征后,实际上我们得到的参数还是非常的多,所以我们采用池化的方法继续减少参数。可以想象一下,训练像素大小为 $96\times96$ 的图片,假设在第一层我们要用 $8\times8$ 学 400 个特征。简单算一下我们就可以发现这层我们就得到了 $89^2 \times 400 = 3168400$ 个参数,其实还是很容易过拟合的。
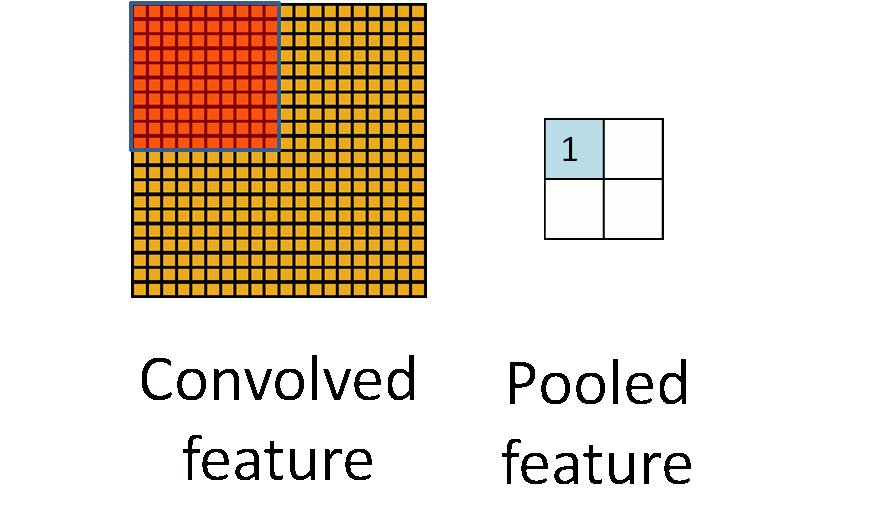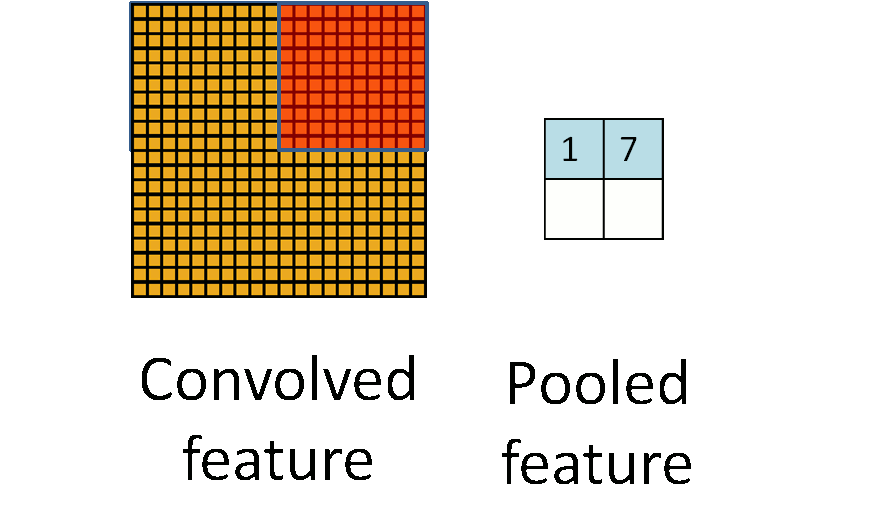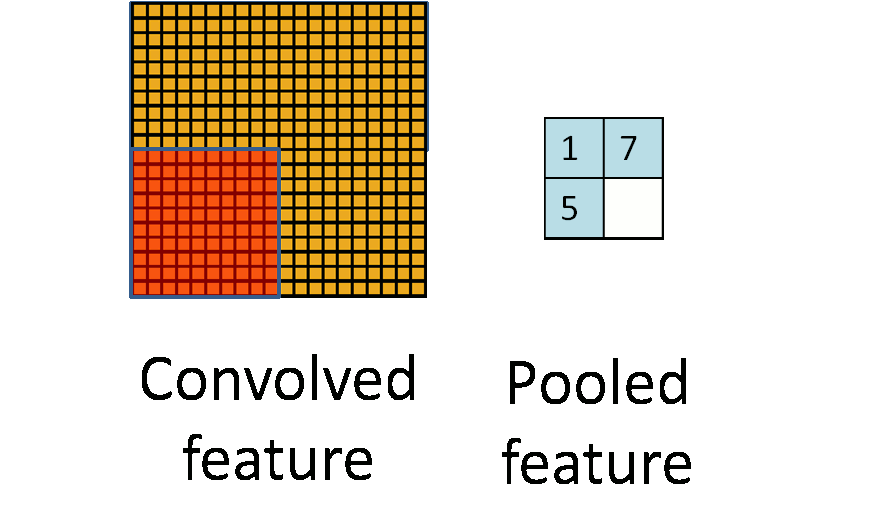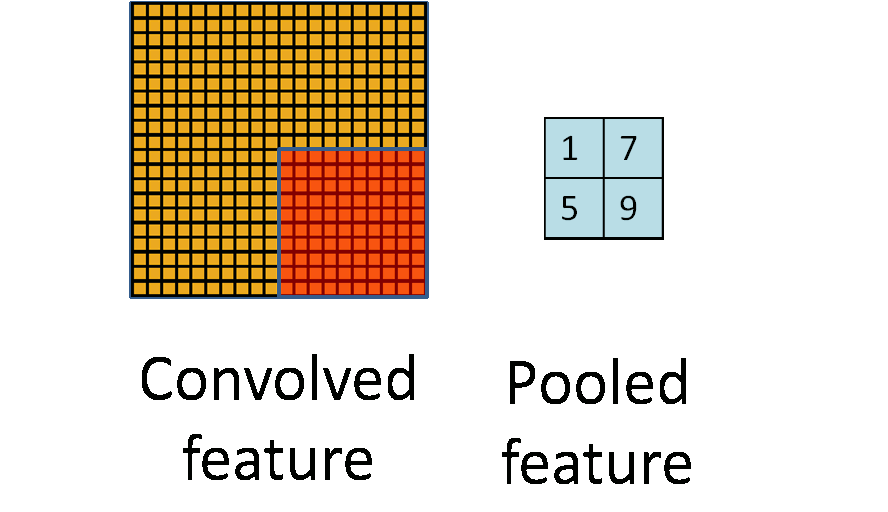
A another good picture worth 1000 words.
据说是由于图像具有稳固性 (Stationarity),也就是说我们可以在一个区域内利用其特征的统计信息进行压缩,或者说是聚焦。上图就是将一个卷积的特征的四个区域压缩到了四个值,大大减少了参数数量,这个步骤我们就成为池化。
常见的池化方法有均值池化 (mean pooling),最大值池化 (max pooling),随机池化 (stochastic pooling)。池化同时也通过统计区域信息,达到了一个降噪的目的,以及平移、旋转、放缩的不变性。
一些著名的卷积网络
LeNet
这是 Yann LeCun 在 1990 左右开发的第一个卷积网络,这个七层神经网络在当时取得了巨大成功,据说当年美国大多数银行就是用它来识别支票上面的手写数字的。
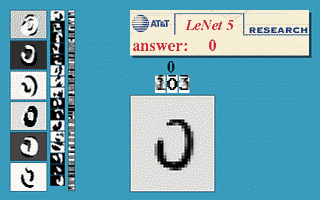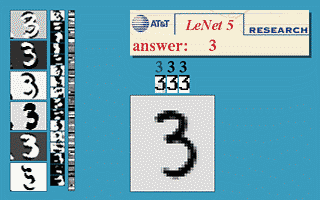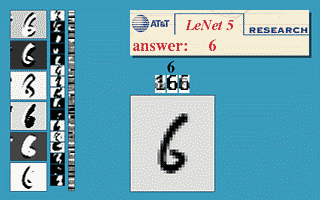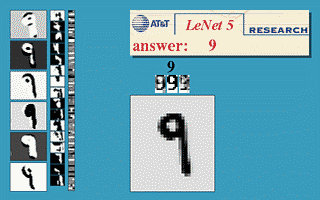
经典的 Lenet-5
AlexNet
这是在 2012 的比赛 ImageNet ILSVRC challenge上由 Alex Krizhevsky, Ilya Sutskever 和 Geoff Hinton 三人设计的深度卷积网络,在比赛中表现出了卓越的性能:Top 5 的错误率是 16% 而亚军是 26%。此网络比 LeNet 很相似但是更深更宽。
ZF Net
这是 Matthew Zeiler 和 Rob Fergus 两人在 2013 年的 ILSVRC 的比赛中获得冠军的网络。这个网络和 AlexNet 很接近,但是做了很多微调,而且在中间的卷积层的规模更大。
GoogLeNet
是谷歌工作人员设计的,在 2014 年的 ILSVRC 比赛中获得冠军,他的主要贡献是开发加初始模块 (Inception Module) 的网络来大大降低了参数的数量,比赛中四百万个参数而 Alexnet 有六千万个。
其中的原理也很简单,GoogLeNet 的构造在原本 $n$ 通道和 $m$ 通道的两层间加入了一个 $p$ 通道的层。
\[n\times m > n\times p + p\times m,\ \ when \ \ p << n\]这个做法不仅降低了参数量和计算量,并且符合神经学的赫布理论 (Hebbian principle),所以在效果上也有不小的提升。
Cells that fire together, wire together –Hebbian Theory
VGGNet
牛津大学的团队 Visual Geometry Group (VGG) 中两人 Karen Simonyan 和 Andrew Zisserman 开发的这个网络获得了 2014 年比赛的亚军,这篇工作的主要贡献是展示了网络深度在获得好的学习性能中的重要作用。VGG 在最终最好的网络包含了 16 层卷积/全连接层,而且更迷人的是所有的特征都统一的在卷积层使用的是 $3\times3$ 的卷积核、在池化层使用的是 $2\times 2$ 的池化。在最后大家发现虽然在分类性能上,它略微逊于 GoogLeNet,但是在多类迁移学习任务 (Multiple transfer learning tasks) 上要更优。所以目前业界在图像处理中还是更倾向于使用这个模型。而且其预训练的模型在平台 Caffe 中可用。但是缺点就是模型中还是有很多的全连接层导致整个模型的训练参数有一千四百万之多 (140M)。
其它网络
Inception 系列的网络就是丧心病狂了,上百层的网络看上去就非常复杂= =,不过可以在 Joseph Paul Cohen 上用 mxnet 工具看到可视化结果。
深度学习工具
深度学习现在已经有很多的工具可以使用,很多框架都非常不多,下面这个表格总结了部分的深度学习工具(来源自微信公众号:深度学习研究会)。
| Name | Primary | Other | Dependencies | Origin | Release | Star |
|---|---|---|---|---|---|---|
| Caffe | C++ | Python | Yangqing Jia | 2013-9 | 6834 | |
| Caffe2 | C++ | Python | CUDA | Yangqing Jia | 2015-6 | 297 |
| cuda-convnet2 | 2015-4 | 182 | ||||
| DeepLearning4j | 2013-11 | 1541 | ||||
| DeepLearnToolbox | Matlab | 2011-10 | 1563 | |||
| Mxnet | MShadow | 2015-4 | 938 | |||
| Pylearn2 | Python | Theano | ||||
| TensorFlow | Python | C++ | 2015-11 | 7057 | ||
| Theano | Python | 2011-8 | 2303 | |||
| Torch | Lua | C | IDIAP | 2013-10 | 3044 |
CNN 的训练
未完待续。。。。
-
Kim, Y. (2014). Convolutional Neural Networks for Sentence Classification ↩