在信息检索或者分类问题中,模型给出结果的好坏需要一个标准的评价度量。大约10年前,在 Machine learning (ML) 文献中一统天下的标准:分类精度 (Accuracy);在信息检索 (IR) 领域中常用 Recall 和 Precision 等等。其实度量反应了人们对“好”的分类结果的追求,同一时期的不同的度量反映了人们对什么是“好”,这个最根本问题的不同认识,而不同时期流行的度量则反映了人们认识事物的深度的变化。近年来,随着 ML 的相关技术从实验室走向实际应用,一些实际的问题对度量标准提出了新的需求。特别的,现实中样本在不同类别上的不均衡分布 (class distribution imbalance problem)。使得 Accuracy 这样的传统的度量标准不能恰当的反应分类器的性能。
举个例子:测试样本中有A类样本90个,B类样本10个。分类器C1把所有的测试样本都分成了A类,分类器C2把A类的90个样本分对了70个,B类的10个样本分对了5个。则C1的分类精度为90%,C2的分类精度为75%。但是,显然C2更有用些。另外,在一些分类问题中犯不同的错误代价是不同的(cost sensitive learning)。这样的话,默认0.5为分类阈值的传统做法也显得不恰当了。
为了解决上述问题,人们从医疗分析领域引入了一种新的分类模型性能评判方法——ROC分析。ROC分析本身就是一个很丰富的内容,搞清楚这些指标我在网上搜索了大量的博客,在这里做了一个小的总结,仅供参考。
准确率,召回率,F1
考虑一个二分问题,即将实例分成正类(Positive)或负类(Negative)。对一个二分问题来说,会出现四种情况:如果一个实例是正类并且也被预测成正类,即为真正类(True Positive);如果实例是负类被预测成正类,称之为假正类(False Positive);相应地,如果实例是负类被预测成负类,称之为真负类(True Negative);正类被预测成负类则为假负类(False Negative)。
TP: 正确肯定的数目
FP: 误报,给出的匹配是不正确的,也叫一型错误 (Type I error)
FN: 漏报,没有正确找到的匹配的数目,
TN: 正确拒绝的非匹配数目
如此就有下图所表示的各类指标的表示,图的中心位置我们称为混淆矩阵 (Confusion Matrix)
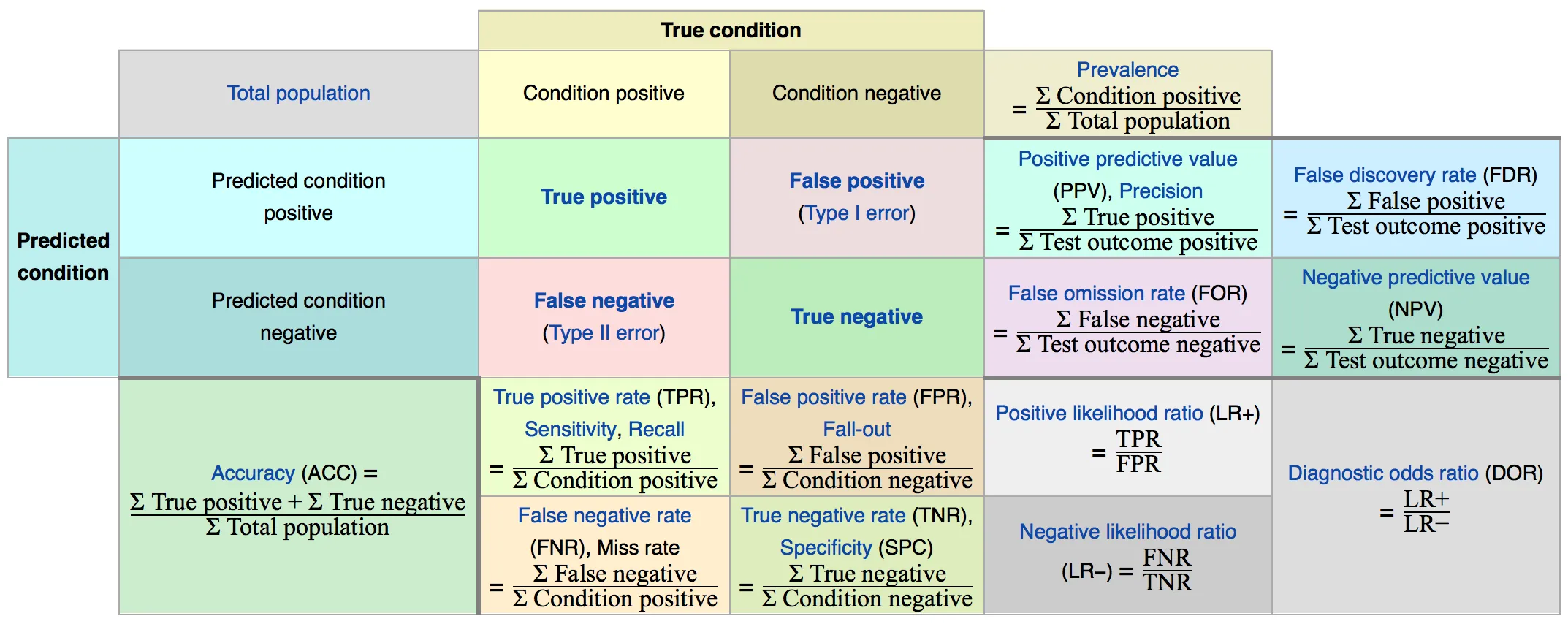
各种性能指标中概览及关系(来源:wikipedia)
图中的各类指标
真正类率 TPR (True Positive Rate)
\[TPR = \frac{TP}{TP + FN}\]即回收率 (Recall),也称为 覆盖率 (Sensitivity),刻画的是分类器所识别出的正实例占所有正实例的比例。
假负类率 FNR (False Negative Rate)
\[FNR = \frac{FN}{TP + FN}\]也叫 丢失率 (Miss Rate),刻画的是分类器错认为负类的正实例占所有正实例的比例。
真负类率 TNR (True Negative Rate)
\[TNR = \frac{TN}{FP + TN}\]即 Specificity (负例的覆盖率),或者叫特异度,刻画的是分类器所识别出的负实例占所有正实例的比例。
理解:Sensitivity 就是灵敏度,是疾病发生后出现症状的概率。Specificity 就是特异度,是疾病不发生时不出现症状的概率。
假正类率 FPR (False Positive Rate)
\[FPR = \frac{FP}{FP + TN}\]也叫 Fall-out,刻画的是分类器错认为正类的负实例占所有负实例的比例。
命中率 PPV (Positive Predictive Value)
\[PPV = \frac{TP}{TP + FP}\]即精度 (Precision)。
准确率 ACC (Accuracy)
\[ACC = \frac{TP + TN}{TP + FP + FN + TN}\]即预测对的数量占总数的比例。
其他
其他还有阳性似然比 LR+ (Positive likelihood ratio)、阴性似然比 LR- (Negative likelihood ratio) 等等。
F1 Score
在二分类问题的统计分析中,F1 Score (也称为 F-score 或者 F-measure) 是分类结果性能测试的一个度量。它综合考虑了精度 (Precision) 和回收率 (Recall) 两个指标去计算新的指标。它的最优理想值是 1,最差理想值是 0.
狭义上的 F-measure 或者说平衡的 F-score (F1 score) 是精度和回收率的调和平均 (harmonic mean)
\[F_1 = 2\cdot\frac{Precision\cdot Recall}{Precision + Recall}\]广义上的 $F_\beta$ 带有一个正实数 $\beta$:
\[F_\beta = (1+\beta^2)\frac{Presicion\cdot Recall}{(\beta^2\cdot Presicion)+Recall}\]还有一个 G-measure 是两者的几何平均:$G = \sqrt{Precision\cdot Recall}$
ROC 曲线
ROC 分析是从医疗分析领域引入的一种新的分类模型评判方法。其全名是 Receiver Operating Characteristic,其主要分析工具是一个画在二维平面上的曲线——ROC curve。平面的横坐标是 False Positive Rate(FPR),纵坐标是 True Positive Rate(TPR)。对取某个阈值 (Threshold) 的分类器而言,可以根据其在测试样本的表现得到一个 TPR 和 FPR 点对。这样,此分类器就可以表示成平面上的一个点。调整这个分类器分类时候使用的阈值,我们就可以得到一个经过 (0,0)-(1,1) 的曲线,这就是此分类器的 ROC 曲线。
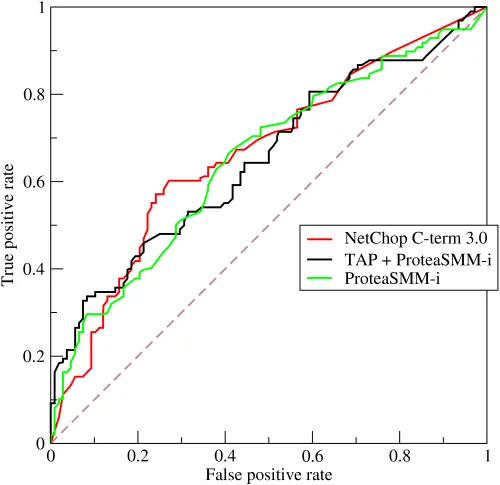
三个预测蛋白酶体的肽切割分类模型的 ROC 曲线 (来源:wikipedia)
一般情况下,这个曲线都应该处于 (0,0) 和 (1,1) 连线的上方。因为 (0,0) 和 (1,1) 连线形成的 ROC 曲线实际上代表的是一个随机分类器 (Baseline Model)。
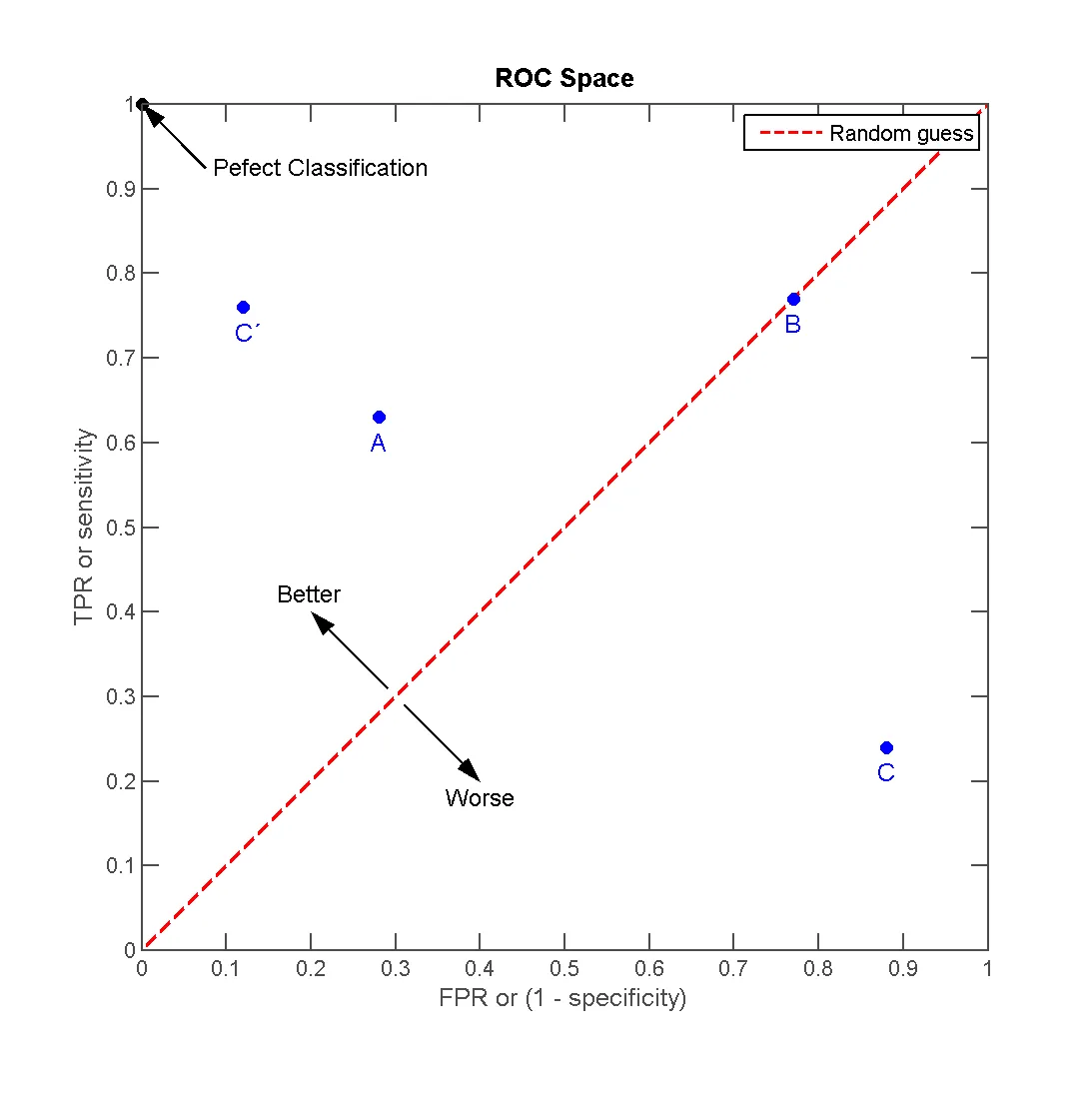
对角线作为基线指示了一个一个分类器的好坏,曲线在上方表示优于随机分类,反之则差。(来源:wikipedia)
在 ROC 空间坐标中,左上角的点,轴 (0,1) 点,这个代表着100%灵敏(没有假阴性)和100%特异(没有假阳性)。而 (0,1) 点被称为完美分类器。
AUC
虽然,用 ROC curve 来表示分类器的性能很直观好用。可是,人们总是希望能有一个数值来标志分类器的好坏。于是 Area Under roc Curve(AUC) 就出现了。
顾名思义,AUC 的值就是处于 ROC curve 下方的那部分面积的大小。通常,AUC 的值介于0.5到1.0之间,较大的 AUC 代表了较好的性能。
以上的性能计算在 Matlab 中的实现也很简单:
[FPR,TPR,Thresh,AUC,OPTROCPT] = perfcurve(labels,scores,posclass)
MAP
MAP (Mean Average Precision) 和 ROC 曲线相似,它对应的是准确率-召回率曲线,其中纵坐标是准确率,横坐标是召回率。其准确定义如下
\[MAP = \int^1_0 {P(R)dR}\]其中 $P,\ R$ 分别代表准确率和召回率,最理想的系统应该包含的面积是 1。